S/Key Dungeon Attack

RFC2289 defines a one-time password system based on a chain of hashes. It is based on S/Key released as RFC1760 by Bellcore, and has found it’s way into many Unix-like distributions. It is still recommended in the FreeBSD security guide

Let’s start with a quick description of the S/Key OTP protocol.

An OTP Client does this:

OTP(0) = H(seed + passphrase)
OTP(1) = H(OTP(0))
OTP(n) = H(OTP(n-1))

What this basically means is that the seed and passphrase are hashed with a one-way cryptographic hash function to produce sequence zero, which is then hashed a number of times - this number is called the sequence. When you initialise your otp chain (or change passwords), you give a copy of sequence 500 (for example - it can be any positive number) to the server. When you want to login for the first time after that you send sequence 499.

An OTP Server does this:

if H(client_otp) == retrieve(previous_otp):
	store(client_otp)
	return Success

Which is to say that the server hashes the OTP provided by the client, and compares it to the OTP stored in the database from the last login. On a successful match, the server replaces the stored OTP with the one provided by the client and allows the login to proceed.

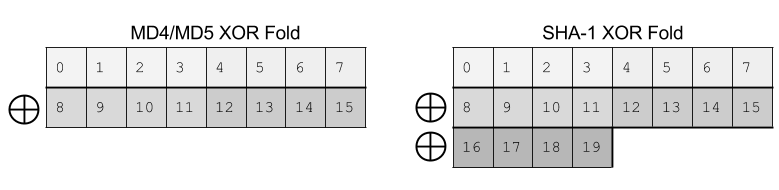
The function H() is defined as being MD4, MD5 or SHA-1, but folded into 64 bits with the XOR operation.

Normally when hashing a password, a salt is used to increase the storage requirements for precomputed hash values and hides from an attacker that multiple users have chosen the same password.

While S/Key includes a salt in the first round (sequence zero) which strengthens it against dictionary attacks and prevents the chain from repeating should somebody reuse a password, it doesn’t include the seed in each round. Combined with the somewhat small 64-bit hash functions this opens S/Key up to a practical time-space trade-off.

Calculating 2⁶⁴ key/value pairs would still take longer than the time between logins for most users on a system. Storing 2⁶⁴ key/value pairs (eg. an ordered table of 2⁶⁴ values) is still fairly large, even by today’s standards. But with this OTP scheme there’s a way to easily compress the storage for a pre-computed attack.

Say you were happy to store 2⁴⁸ 64-bit key/value pairs on disk, you could store each OTP sequence 2¹⁶ of an arbitrary value. This would cover most of the 64-bit space (you will lose some coverage due to collisions and overlapping sequences. Shorter sequences mean less collisions). Assuming 32 bytes per hash (including indexing overhead), that would require 35TB of storage, plus enough CPU/GPU time to once-off calculate 2⁶⁴ values. Storing less will result in having a smaller probability of breaking the intercepted OTP - you’ll just need to intercept more to get a break.

When you intercept an OTP, check if it is in the table. If so, you simply need to hash your original value 2¹⁶-1 times (sticking with our example numbers from before) and you have an OTP that will work. In fact at that point you could probably log in 65535 times if the server isn’t keeping an eye on the sequence number.

If you didn’t find the hash on your first try then not all is lost - simply hash the intercepted OTP and check if that’s in the table. If so then you hash the value in your table 2¹⁶-2 times. You can repeat this process up to 2¹⁶-1 times before giving up.

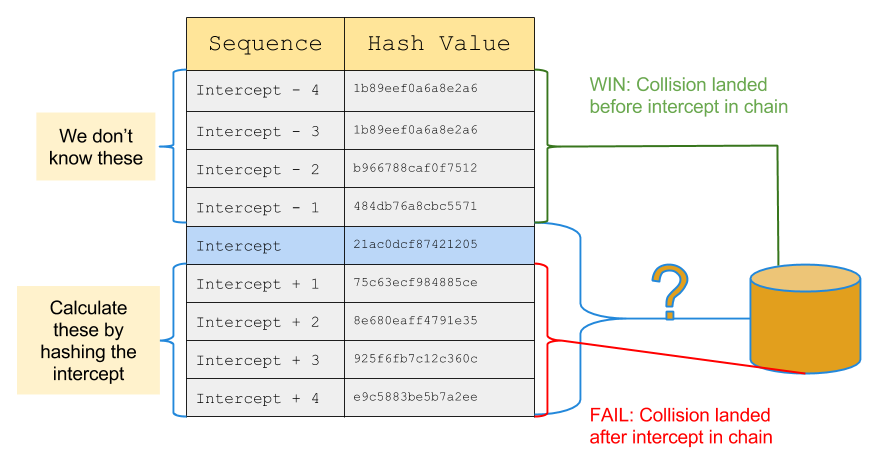
You can trade off time vs space almost arbitrarily with this attack, although it still assumes that you’re willing to pre-compute 2⁶⁴ values. Keep in mind that storing excessively large chains will result in convergence. I found 2¹⁶ is a good value, and 2²⁸ is extremely convergent.

I’ve added some code to GitHub for anyone wishing to try out this technique. Please let me know how you go.

Examination of a break:

Included below is some code that examines a collision I found using this technique:

#!/usr/bin/python3
 
from binascii import a2b_hex as unhex, b2a_hex as mkhex
import hashlib
import numpy
 
# Grab the cotpmd5 module from:
# https://github.com/therealmik/otpbreak/tree/master/pyotpmd5
import cotpmd5
 
def hex_to_np(h):
    """Convert 64-bits of hex string into a numpy.uint64"""
    assert(len(h) == 16)
    return numpy.fromstring(unhex(h), dtype=numpy.uint64)[0]
 
def np_to_hex(n):
    """Convert a numpy.dtype into a hex string"""
    return str(mkhex(n.tostring()), "US-ASCII")
 
def create_seq_zero(seed, password):
    """Perform the initial part of the OTP calculation"""
    h = hashlib.md5(seed + password).digest()
    n = numpy.fromstring(h, dtype=numpy.uint64)
    return n[0] ^ n[1]
 
seed=b'hn70134'
seq=50
password=b'8dCOU97AVK9HjSiX'
seqzero = create_seq_zero(seed, password)
orig_chain = cotpmd5.otpmd5_chain(seqzero, 50)
 
collision=hex_to_np('31af346a00000000')
collision_index=29848
collision_chain = cotpmd5.otpmd5_chain(collision, collision_index)
 
for i in range(25):
    print(np_to_hex(orig_chain[-25 + i]), np_to_hex(collision_chain[-25 + i]))

Output:

aee35ed8d024524e 9d2a44466ba5e04c
30cd16dd5e4e43af b73d20de3ff02282
7cd5de8a09cc2055 63d59b54ac13c692
773b713d8f1f5ebf 773b713d8f1f5ebf
f5efb81a79cb8ffc f5efb81a79cb8ffc
19d6256e61984dc0 19d6256e61984dc0
69c0aadb6ba9503c 69c0aadb6ba9503c
5101c2d589fc03c8 5101c2d589fc03c8
a5d4ca9beb2ba353 a5d4ca9beb2ba353
0ba6a04be986d0b2 0ba6a04be986d0b2
eba961fc7271d430 eba961fc7271d430
92a9849b06a42a86 92a9849b06a42a86
26fcbea549e10fd0 26fcbea549e10fd0
374d5fe2ccdc1be4 374d5fe2ccdc1be4
de72b854776cf3dc de72b854776cf3dc
5069844461617ec2 5069844461617ec2
b432a39719c92062 b432a39719c92062
632bf7b4058d49c7 632bf7b4058d49c7
39c2d5fa73b84d29 39c2d5fa73b84d29
6a6d7c9763a5b439 6a6d7c9763a5b439
bbde20e23066f8e4 bbde20e23066f8e4
1b89eef0a6a8e2a6 1b89eef0a6a8e2a6
b966788caf0f7512 b966788caf0f7512
484db76a8cbc5571 484db76a8cbc5571
21ac0dcf87421205 21ac0dcf87421205

This was presented as part of my Ruxcon 2013 talk Under the hood of your password generator. I also presented on TOTP and Random password generators