How Random Password Generators Can Fail

#Introduction

Passwords are an awkward security model. The idea was simple at first - you remember something that nobody else can guess. Unfortunately our associative memory makes this hard - either passwords are easy to guess, or they’re impossible to remember. We’re not allowed to use the same or a similar password for all the different systems we use (possibly tens or hundreds of websites!) - we have to remember another completely unrelated random string for everything we do.

Now you could wait for something better to come along like smart card authentication or OTP tokens, but webmasters are a slow-moving beast when it comes to security technology. The best thing to do is simply to use a random password generator and store them somewhere safe. I’m not going to recommend any particular storage solution in this article - that’s a whole different essay.

It is unfortunate that not all random password generators were written with a clear understanding of how to generate unguessable passwords. Let’s take a look at a few examples.

#Awesome Password Generator

The sysadmin team at work use random password generators constantly - it’s just part of the work flow for a lot of what we do. For production systems, they go straight into the password management system, but for lab systems or temporary accounts, we just generate one and send it across.

So when the new guy (at the time) sent me a password that looked hinky, I asked him what program he used to generate it. It turns out he was using Awesome Password Generator.

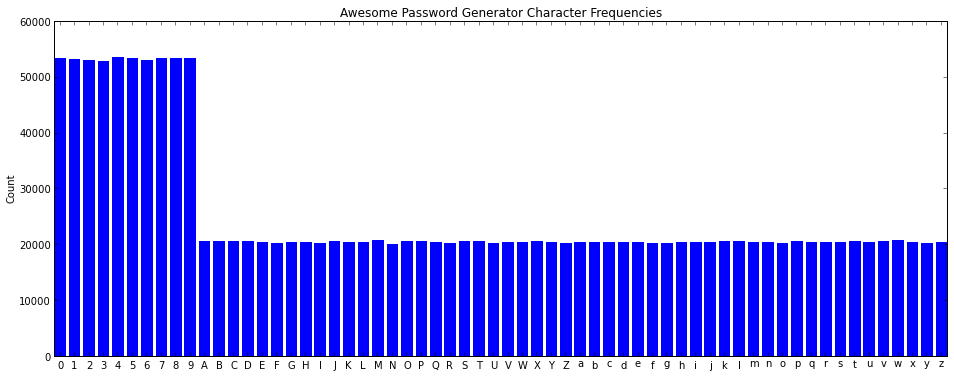
When looking at the output of anything that should have a random distribution, the first thing to do is to look for bias - and the fastest way to do that is to collect a lot of output and generate a histogram.

Here’s a histogram of the Awesome Password Generator (1.3.2) output:

Let’s take a look at the code that’s causing this bias - I trimmed the code and rewrote the comments below:

while (true) {
	// Select password_length numbers in the range {0..numCharSets}
	// numCharSets = 3 for the histogram above
	for (i = 0; i < pgo.pswLength; i++) {
		pswLayout[i] = rnd.Next(0, workCharsets.Length);
	}

	// Check that each charset was used (in a funny way), so long as
	// the password length allows.
	int usedCharGroupsCnt = 0;
	for (i = 0; i < pgo.pswLength; i++)
		if (pswLayout.Contains(i)) usedCharGroupsCnt++;
	if (usedCharGroupsCnt == Math.Min(workCharsets.Length, pgo.pswLength)) break;
}

string psw = "";
for (i = 0; i < pgo.pswLength; i++) {
	// Select a random character from the chosen character set
	psw += workCharsets[pswLayout[i]][rnd.Next(0, workCharsets[pswLayout[i]].Length)];
}

What it’s doing is selecting which type of character belongs in each position of the generated password, then selecting the character from that group. Since the character sets are different lengths, that means that the number 5 is much more likely than the letter F.

To understand why this causes bias let’s work out the probability of each character being selected. We start with a probability of 1.0 of any character being selected. Now we divide by 3 - since there are 3 classes (uppercase/lowercase/number) that are being selected from for each position. Finally, we divide the numbers by 10 and the letters by 26. That means that each of the numbers have a 3.3% chance of being selected, while letters have a 1.3% chance of being selected.

The bias is interesting, but while digging around I found an even worse problem - one which would allow all passwords generated to be cracked in a reasonable amount of time.

Have a look at this piece of code:

// initialize Random class
byte[] dwSeed = new byte[4];
rng.GetBytes(dwSeed);
int iSeed = BitConverter.ToInt32(dwSeed, 0);
Random rnd = new Random(iSeed);

It turns out that the Cryptographic RNG class variable was only used to get 4 bytes (32 bits) of entropy, then it seeds the Windows System.Random() RNG. This is actually twice as bad as it seems because System.Random() converts negative seeds into positive seeds - resulting in only 2³¹ possible seed values.

This is easily exploited against hashed passwords - particularly for fast hashes that are easily intercepted, such as Digest Authentication or NTLM.

I contributed an External Mode for John the Ripper, which can be viewed here. It simply goes through all 2³¹ seed values and generates the password that would result.

This has all been fixed in version 1.4.0, so if you have been using Awesome Password Generator, I encourage you to download the lastest version then go change all of your passwords. The lastest version is all good, but I don’t recommend easy to type mode. I get the feeling that the author (Alex) has a pretty good understanding of password generation now - I’d be surprised to find repeat problems in future versions.

#pwgen

For a program that I have used so many times for so many years, it amazes me how ambivelant I was to it’s security. The command ‘pwgen -s 16’ comes out of my fingers faster than I can think it.

####CVE-2013-4442 pwgen Silent fallback to insecure entropy After being chided by a co-worker (who’s favourite password generator I’d just thoroughly ruined for him) I thought I’d open the source of pwgen and just check the basics.

The first thing I found was this:

static int get_random_fd()
{
        struct timeval  tv;
        static int      fd = -2;
        int             i;

        if (fd == -2) {
                gettimeofday(&tv, 0);
                fd = open("/dev/urandom", O_RDONLY);
                if (fd == -1)
                        fd = open("/dev/random", O_RDONLY | O_NONBLOCK);
#ifdef HAVE_DRAND48
                srand48((tv.tv_sec<<9) ^ (getpgrp()<<15) ^
                        (getpid()) ^ (tv.tv_usec>>11));
#else
                srandom((getpid() << 16) ^ (getpgrp() << 8) ^ getuid() 
                      ^ tv.tv_sec ^ tv.tv_usec);
#endif
        }
        /* Crank the random number generator a few times */
        gettimeofday(&tv, 0);
        for (i = (tv.tv_sec ^ tv.tv_usec) & 0x1F; i > 0; i--)
#ifdef HAVE_DRAND48
                drand48();
#else
                random();
#endif
        return fd;
}

Under normal circumstances it uses /dev/urandom - a Linux system without the /dev/urandom device file is horribly broken. But in abnormal circumstances (such as AppArmor or SELinux mis-configurations), it would fall-back to srand48() without printing an error.

We know by now that a 32-bit seed really doesn’t cut it but what’s interesting is that the values passed to the seed aren’t really all that secret.

For example, the most-significant 11 bits of tv.tv_sec is a 48-day time window - something that a password expiry field is sure to give away.

The pid and pgrp are the same for the general case of somebody calling it from an interactive shell without any pipes, and the most chaotic 11 bits of tv_usec are being discarded.

Note that an 5 extra bits of entropy are (sortof) added by the “cranking” based on a new timestamp/usec value.

####CVE-2013-4441 pwgen Phonemes mode has heavy bias and is enabled by default

While reporting this to the oss-security mailing list, I made an offhand comment about phonemes mode (without any data to back it up). Solar Designer replied to my message, asking if I’d seen a previous thread on the matter.

I hadn’t seen it, but it piqued my interest.

Before I explain what further work I added to Solar Designer’s (read that thread if you haven’t already!), I’ll explain the basics of what a phoneme is.

The idea is to produce pronouncible passwords. This is done by having a list of letters, numbers and diphthongs (with a missing ‘h’ in the code - search for DIPTHONG). A diphthong is a pair of letters that form a sound as if they were a single letter, such as “ie”.

The code is pretty complicated, but it basically has some rules to decide whether it can be uppercase, a number, a vowel/consonant, and whether the vowel/consonant can be a diphthong pair.

Here’s the resulting bias:

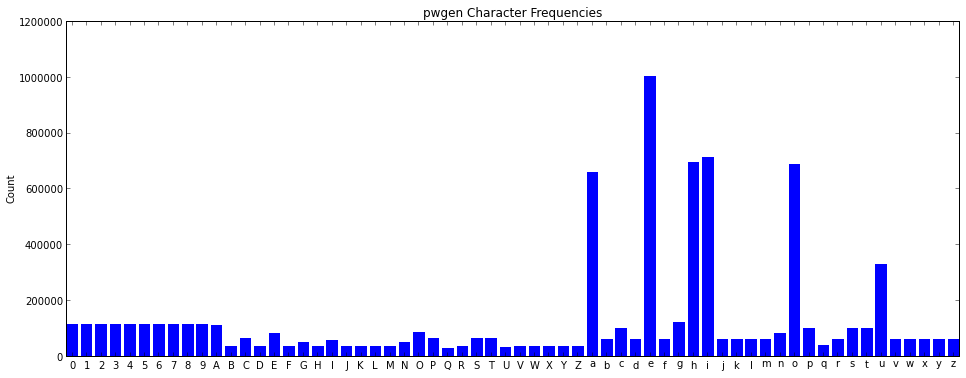
At first I thought it would be a simple task - I would generate all possible pwgen phonemes, by rewriting the core as a recursive python generator expression. Furthermore, I’d add actual probabilities to the generated phonemes, and spit them out in order.

This was a time consuming task, and hard to verify. You can see my results here - the probabilities are out (according to my emperical tests), but tests on shorter password lengths show that it does seem to generate all of them.

I also had to merge the paths of vowel-diphthong pairs such as “ie”, which can also be generated by producing “i” then “e”. This is a double-whammy for bias - not only is the “ie” pair consuming 2 character positions compared to selecting a single character - resulting in less entropy per character, but there are actually two separate code-paths that lead to identical phonemes. Some passwords can in-fact have 3 of these double-paths in them, resulting in 8 different ways to generate the same word!

If my code is correct, there are 1175,721,794,250 (just over 2⁴⁰) 8-character phonemes.

####CVE-2013-4440 pwgen non-tty passwords are trivially weak by default If you run pwgen on the command-line, you get a mix of upper-case, lower-case and numbers in your phonemes. While phonemes mode by default is bad, if you’d been piping the output of pwgen into another program (eg. pwgen | less), it deselects numbers and upper-case by default, resulting in horribly weak passwords.

#KDE Paste Applet

Once every few months I try switching my desktop environment to KDE4, hoping that it’s finally as awesome as KDE3 was. This never lasts long, but I do take the time to try out new widgets and apps - the KDE folks have brought some of the best innovations to the Linux desktop.

One widget that caught my attention was the Paste applet - this simple applet seemed mostly useless to me, except for the “Random Password” thing it had. By this time I’d already picked apart countless random password generators and really couldn’t start using another one without checking the code.

Here’s what I found:

QString PasteMacroExpander::password(const QString& args)
{
   static QStringList characterSets = QStringList()
           << "abcdefghijklmnopqrstuvwxyz"
           << "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
           << "01234567890"
           << "!\"#$%&'()*+,-./:;<=>?@[\\]^_`{|}~";

   // [ Code that parses args cut out ]

   QDateTime now = QDateTime::currentDateTime();
   qsrand(now.toTime_t() / now.time().msec());
   for (int i = 0; i < charCount; ++i) {
       result += chars[qrand() % chars.count()];
   }
   return result;
}

So the first thing you won’t notice is that the number 0 appears twice in the list of numbers. That’s a minor source of bias, but it’s easily fixed and probably not going to give too much advantage to an attacker.

Another trivial source of bias is the modulo operator - if the remainder of the maximum value of qrand() isn’t a multiple of chars.count(), there’ll be a really tiny bias towards the first characters in the set.

####CVE-2013-2120 Finally we get to the exploitable vulnerability - qrand() is just a wrapper around rand_r(), which has only 32-bits of state. That means that if you call qrand() multiple times like here, it still has at-most 2³² possible strings it could generate.

But we can do better than 2³² here - look at how it’s seeding qsrand(). It’s using a timestamp with milliseconds. The seconds is easy

• there’s only 31536000 seconds in a year, and if we found something like a password expiry we could narrow it down to quite a small period of time.

The choice of division by the milliseconds value is an interesting one - there are only 999 possible values of the milliseconds, because whenever 0 was returned the program would crash - surely a Dr Konqui report must’ve come in for that!

While we do have to try all possible millisecond values, the division has discarded some entropy from the timestamp. So what we can do is generate an extra 1000 seconds worth of timestamps, but now only generate seeds for when seconds mod milliseconds is 0. This effectively cuts the milliseconds out of the complexity - we’re back to just caring about the number of seconds.

You can find the JtR External Mode to exploit this here.

####CVE-2013-2213 So I guess this story should end with the KDE folks fixing this and it being upstreamed into all of the Linux distributions. Well they did change the code, and it did get upstreamed into Fedora and Ubuntu - but the fix was to use KRandom::random().

Here’s the code for that function:

int KRandom::random()
{
   static bool init = false;
   if (!init)
   {
      unsigned int seed;
      init = true;
      int fd = open("/dev/urandom", O_RDONLY);
      if (fd < 0 || ::read(fd, &seed, sizeof(seed)) != sizeof(seed))
      {
            // No /dev/urandom... try something else.
            srand(getpid());
            seed = rand()+time(0);
      }
      if (fd >= 0) close(fd);
      srand(seed);
   }
   return rand();
}

This was presented as part of my Ruxcon 2013 talk Under the hood of your password generator. I also presented on TOTP and S/Key